D A R K T R U T H

假設有100個人，每個人都有100元的本錢，讓他們玩一個遊戲。每輪遊戲中，每個人都要拿出1元，並「隨機」給另一個人，總共進行17,000輪。這個實驗的製作，主要是為了模擬世界的財富運行規律。實驗假設：每個人在18歲時帶著100元的初始資金開始玩遊戲，每天玩一次，一直玩到65歲退休。如此計算，人一生要玩17,000次遊戲，即獲得17,000次財富重分配的機會。每個人「每天拿出1元」可解釋為基本的日常消費，而這「日常的消費」則以隨機的方式，移動到另一個人身上，代表每個人透過複雜的經濟活動而獲得財富的隨機概率。那麼，最後這100人的財富分佈會變成什麼樣呢？接近平均分佈？還是出現貧富差距？而這個實驗，能夠帶給我們的啟示又是什麼呢？

經過公正的機率計算，遊戲運行17,000次的結果如下：

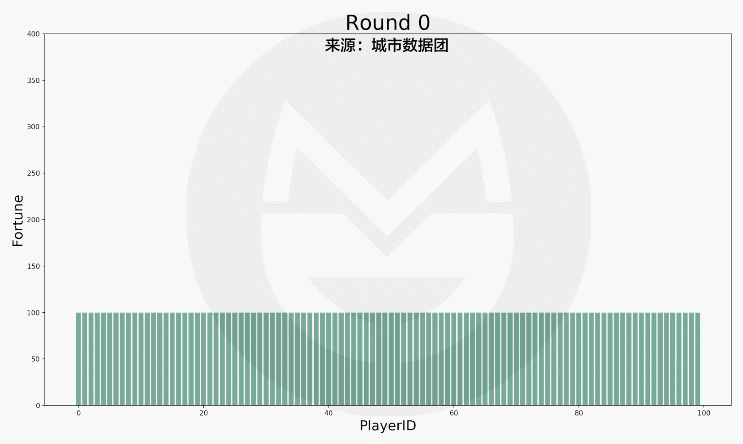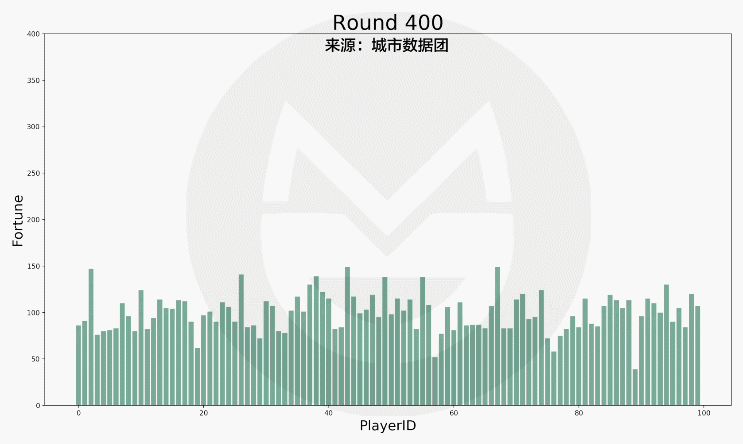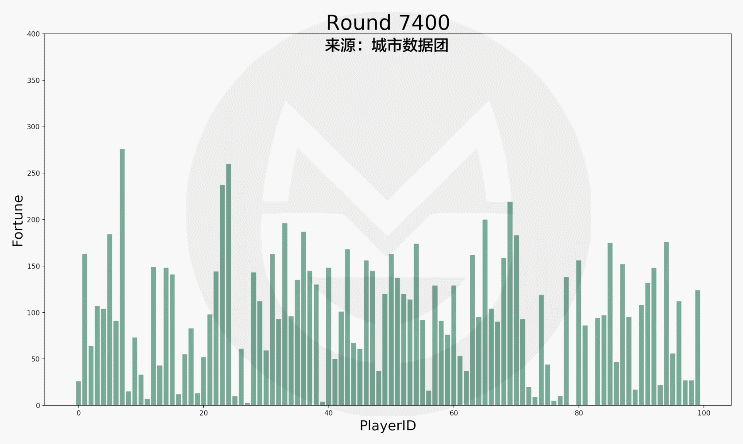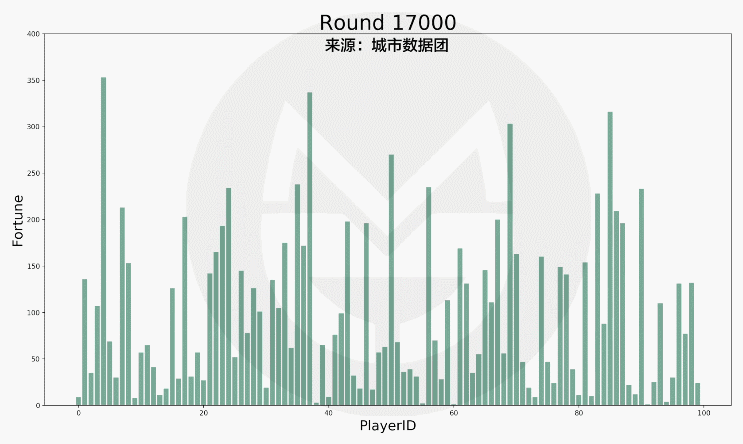
如圖所見，每個玩家的財富變動的非常劇烈。而如果我們把它按照數值多寡進行排序，結果如下：

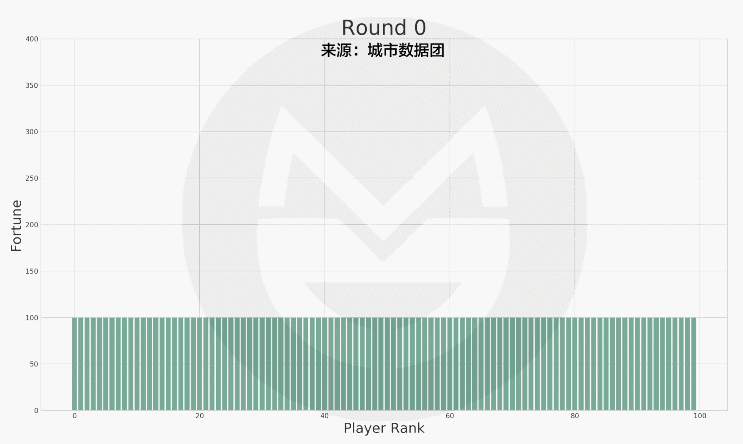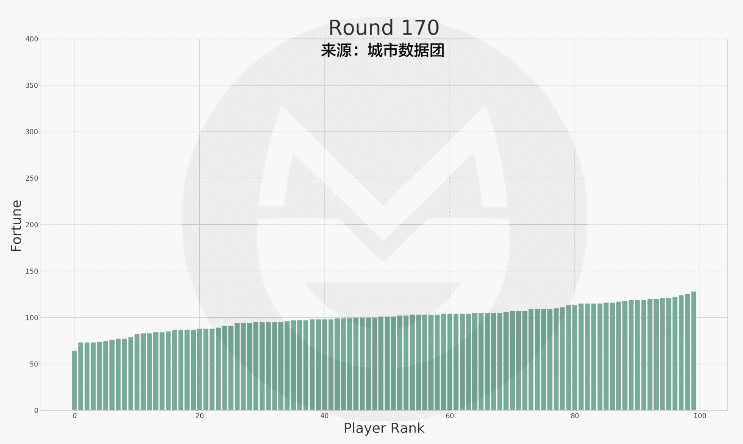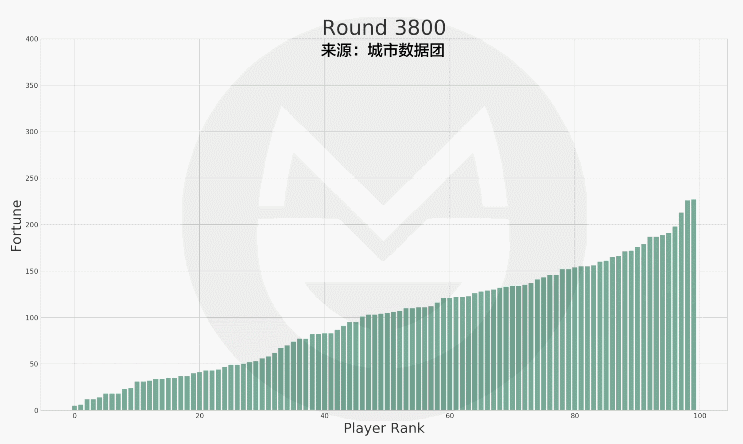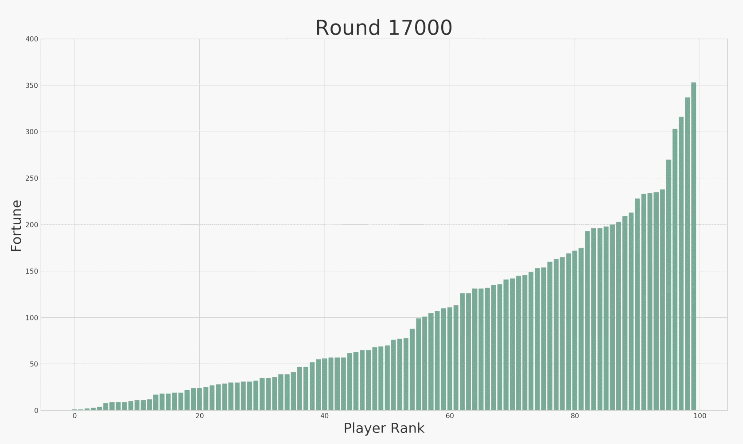
結果和您想像的一樣？還是很不一樣呢？

結果顯示：Top 10%的人掌握了約30%的總財富、Top 20%的人掌握了約50%總財富，而超過60%的人財富所縮水到100元以下。

然而，從這17,000次的模擬實驗中，還可以發現一個現象，那就是貧富差距的急劇拉大，主要發生在第6,000~6,500次之前，以我們前面所假設的18歲到65歲共17,000天來說，第6,000~6,500次差不多就是35歲的前後。

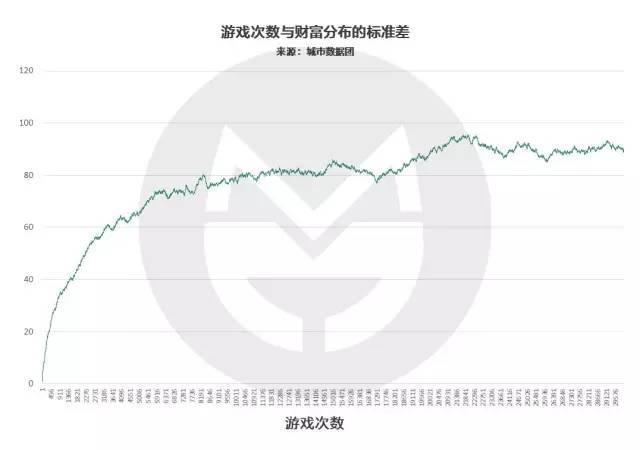
（說明：橫軸表示遊戲輪數，縱軸表示社會財富的標準差）

我們發現，遊戲早期的標準差變動最為激烈，而在6,000-6,500輪後，標準差的變化趨於平緩，也就是社會財富分佈的總體形態趨於穩定了。按照我們設定的遊戲與人生的對應規則，此時玩家的年齡為35歲。

然後，原本的模擬實驗中，如果在17,000次的財富重分配過程中，身上剩下0元的人，是被設定為不用付出1元的。但如果我們把實驗中加入「允許負債」的話，會變成什麼樣呢？

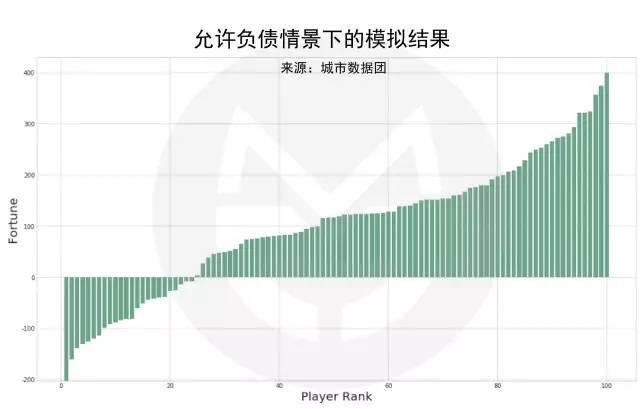
加入「允許負債」的設定後，Top10%的人掌握著大約33%的財富，Top20%的人掌握著大約56%的財富；而大約25%的人會呈現負債狀態。

而如果再把「允許負債」以及「35歲左右財富排位大致底定」這兩個因素一併來看的話，我們可以發現，如果在35歲時破產（資產在0以下）的玩家，在35歲以後能夠「重回水面上」的機率，只有不到50%。而且那些「重回水面上」的，也絕大多數都排在「有產階級」的中下層。

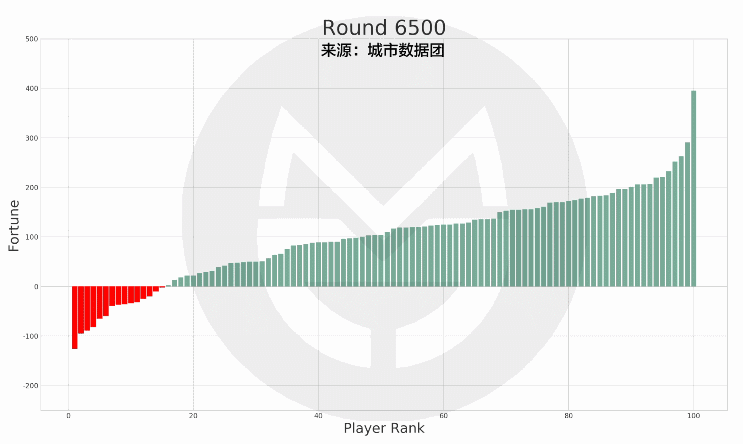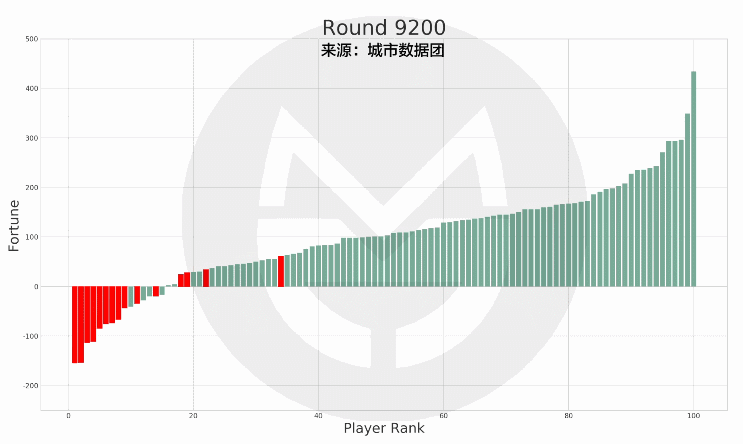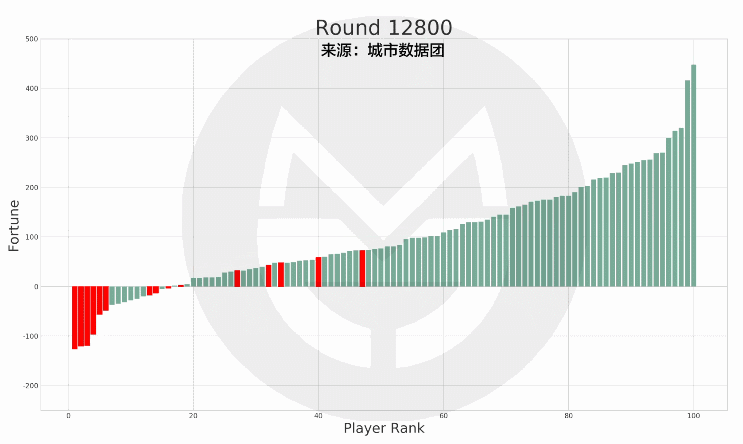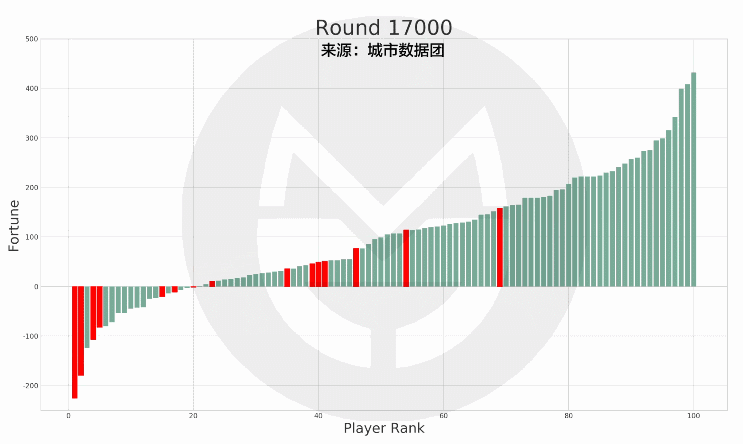
（說明：上圖中的紅色柱子為在35歲時破產的玩家，綠色柱子為其他玩家。紅色柱子在縱軸上的高度變化表示其財富值變化，在橫軸上的位置變化表示其排名變化。）

然後，如果我們把這個實驗再進行round 2，會產生什麼樣的結果呢？

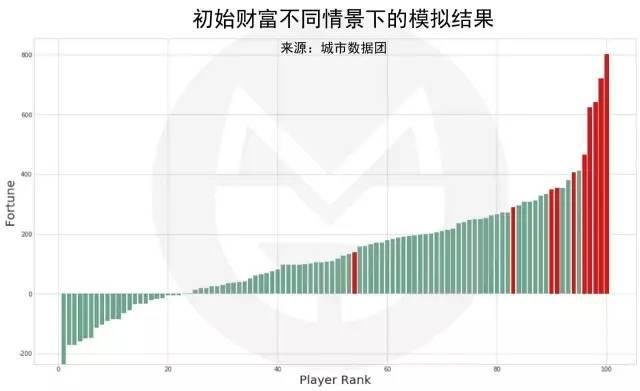
Round 2結束之後，雖然財富的分佈狀態還是和Round 1差不多，但是可以從圖中的紅色柱子看出一些端倪：被標註為紅色的是Round 1的Top 10贏家，我們可以發現，Round 2裡的Top 10贏家，有7位來自於 Round 1的Top 10，而Round 2裡的Top 5，更是全部出自於Round 1的Top 10。

我們再把富二代玩家（紅色線條）和普通玩家（綠色線條）中各選5位，繪製出他們的財富值變化圖：

可以看到，富二代玩家中雖然也有「敗家子」，但他們仍有很大的機率，將人生的最終總財富值，維持在整體社會中的高水平。而普通人則要有極好的運氣，才能到達與敗家富二代相同的高度。

看完這個實驗後，能給我們什麼樣的啟示呢？請繼續閱讀【數據下的殘酷世界 努力就能贏過富二代嗎？】一文。